Home / Construction / Correspondence between a slope in % and a slope in ° (español – français)
How to calculate the dimensions of a roof pitch in degrees or %?
Share this page
What is a roof slope?
The slope of a roof is determined according to several parameters:
- the geographic location,
- the constraints of exposure to wind, snow/rain,
- the constraints of urban planning and aesthetics,
- the roofing materials used,
- the size of the roof
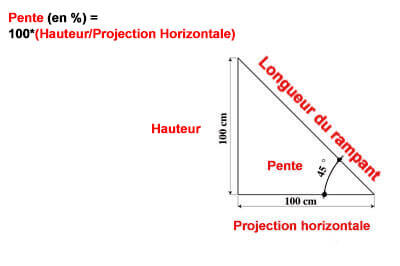
The slope of the framework also determines the strength of the structure. The roof pitch is the angle between the inclination of the roofing and the horizontal projection. (length of the slope, horizontal projection, slope)
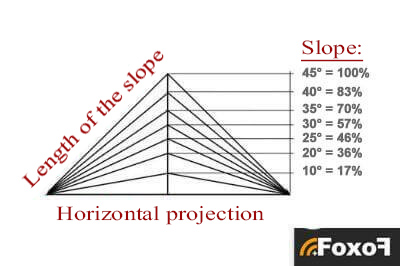
Diagram of a 2-sided roof slope
How to calculate the slope in % or in °?
Example:
- Height (highest point) = 2 meters
- Horizontal projection = 4 meters
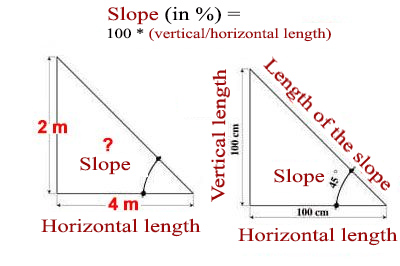
+ The roof pitch in percentage = P in % = 100*(Height/Horizontal Projection)
- Example of the Pitch = 100*(2/4) = 50%
+ The roof pitch in degrees = P in ° = Arctangent(Height/
- If you have the dimensions => Slope = Arctangent(2/4) x (180/π) = 26.56° (ps: (180/π) transforms the angle to radians in °)
- If you have the slope in % => Slope = Arctangent(0.2125) x (180/π) = 12° (ps: 0.2125 corresponds to a slope of 21.25%)
Table of correspondences between ° and % of roof slope
This table allows you to obtain:
- the correspondence of a roof slope in ° or in %
- the value of the ridge height for a given roof slope… for a given horizontal projection.
The horizontal projection is a half range, i.e. horizontal distance between the centre of the ridge and the outer side of the wall plate.
| ° of slope | % of slope | Correspondence for 1 meter of half-range |
| 5° | 9% | for 1 horizontally advanced meter we rise for 9 cm |
| 10° | 17.63% | for 1 horizontally advanced meter we rise for 17,63 cm |
| 11° | 19.43% | for 1 horizontally advanced meter we rise for 19,43 cm |
| 12° | 21.25% | for 1 horizontally advanced meter we rise for 21,25 cm |
| 13° | 23.08% | for 1 horizontally advanced meter we rise for 23,08 cm |
| 14° | 24.93% | for 1 horizontally advanced meter we rise for 24,93 cm |
| 15° | 26.79% | for 1 horizontally advanced meter we rise for 26,79 cm |
| 16° | 28.67% | for 1 horizontally advanced meter we rise for 28,67 cm |
| 17° | 30.57% | for 1 horizontally advanced meter we rise for 30,57 cm |
| 18° | 32.49% | for 1 horizontally advanced meter we rise for 32,49 cm |
| 19° | 34.43% | for 1 horizontally advanced meter we rise for 34,43 cm |
| 20° | 36.39% | for 1 horizontally advanced meter we rise for 36,39 cm |
| 21° | 38.38% | for 1 horizontally advanced meter we rise for 38,38 cm |
| 22° | 40.40% | for 1 horizontally advanced meter we rise for 40,40 cm |
| 23° | 42.44% | for 1 horizontally advanced meter we rise for 42,44 cm |
| 24° | 44.52% | for 1 horizontally advanced meter we rise for 44,52 cm |
| 25° | 46.63% | for 1 horizontally advanced meter we rise for 46,63 cm |
| 26° | 48.77% | for 1 horizontally advanced meter we rise for 48,77 cm |
| 27° | 50.95% | for 1 horizontally advanced meter we rise for 50,95 cm |
| 28° | 53.17% | for 1 horizontally advanced meter we rise for 53,17 cm |
| 29° | 55.43% | for 1 horizontally advanced meter we rise for 55,43 cm |
| 30° | 57.73% | for 1 horizontally advanced meter we rise for 57,73 cm |
| 31° | 60.08% | for 1 horizontally advanced meter we rise for 60,08 cm |
| 32° | 62.48% | for 1 horizontally advanced meter we rise for 62,48 cm |
| 33° | 64.94% | for 1 horizontally advanced meter we rise for 64,94 cm |
| 34° | 67.45% | for 1 horizontally advanced meter we rise for 67,45 cm |
| 35° | 70.02% | for 1 horizontally advanced meter we rise for 70,02 cm |
| 36° | 72.65% | for 1 horizontally advanced meter we rise for 72,65 cm |
| 37° | 75.35% | for 1 horizontally advanced meter we rise for 75,35 cm |
| 38° | 78.12% | for 1 horizontally advanced meter we rise for 78,12 cm |
| 39° | 80.97% | for 1 horizontally advanced meter we rise for 80,97 cm |
| 40° | 83.90% | for 1 horizontally advanced meter we rise for 83,90 cm |
| 41° | 86.93% | for 1 horizontally advanced meter we rise for 86,93 cm |
| 42° | 90.04% | for 1 horizontally advanced meter we rise for 90,04 cm |
| 43° | 93.25% | for 1 horizontally advanced meter we rise for 93,25 cm |
| 44° | 96.57% | for 1 horizontally advanced meter we rise for 96,57 cm |
| 45° | 100% | for 1 horizontally advanced meter we rise for 100 cm |
How to calculate the height of the ridge?
To determine the height of the ridge for a given angle, multiply the figure in column 3 by the value of the horizontal projection (half-range).
For example, if the local regulation and parameters impose a roof slope of 25°:
- for a half-range distance of 4 meters (ex: the housing is 8 meters wide in the case of a symmetrical 2-sided roof)
- the height of the ridge will be 46,63 cm x 4 = 186 cm
How to calculate the length of the slope?
To determine the length of the slope (i.e. the hypotenuse of right triangle):
Length of the slope = √ [(half-range)²+(height of the ridge)²]

Practical case n° 1: How to create an annex with the same roof slope as your house?
For aesthetic or regulatory reasons, you may wish to create an annex building with a slope identical to that of the main building. If you don’t know the angle, how to proceed?
Steps:
- Discover an area of about 1 m2 of the existing roofing of the main building if it is made of tiles. If it is made of slate there’s nothing to discover.
- Cut a piece of wood (batten) of 100 cm. Place the batten horizontally on the roof (using a level) until one of its ends touches the roof covering (or a lath or a rafter).
- With a measuring tape measure the height between the other end of the batten and the roof covering (run the tape perpendicularly from the end of the batten downwards to the roofing). Make sure to respect the vertical.
- The value of this measure will allow you to determine the slope:
- e.g.: 25 cm. The slope in % will be = 25 cm / 100 cm = 25%
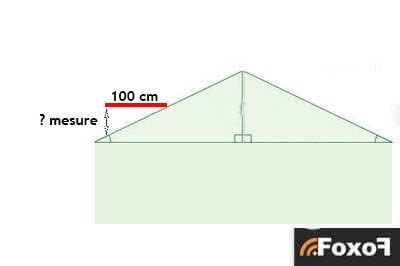
Ps: if the attic is fitted or accessible you will be able to reproduce the same method from inside of the housing (without going up on the roof!).
vous serez en mesure de reproduire la même méthode depuis l’intérieur du logement (sans monter sur le toit !).
Other subjects that may be of interest to you
To know more about The best insulations for construction
To know more about The best heaters
To know more about The difference between room temperature and apparent temperature
To know more about The identification of thermal bridges and the prevention of mould
EN-FOX53